Geometrische Formeln - Fläche, Umfang und Volumen

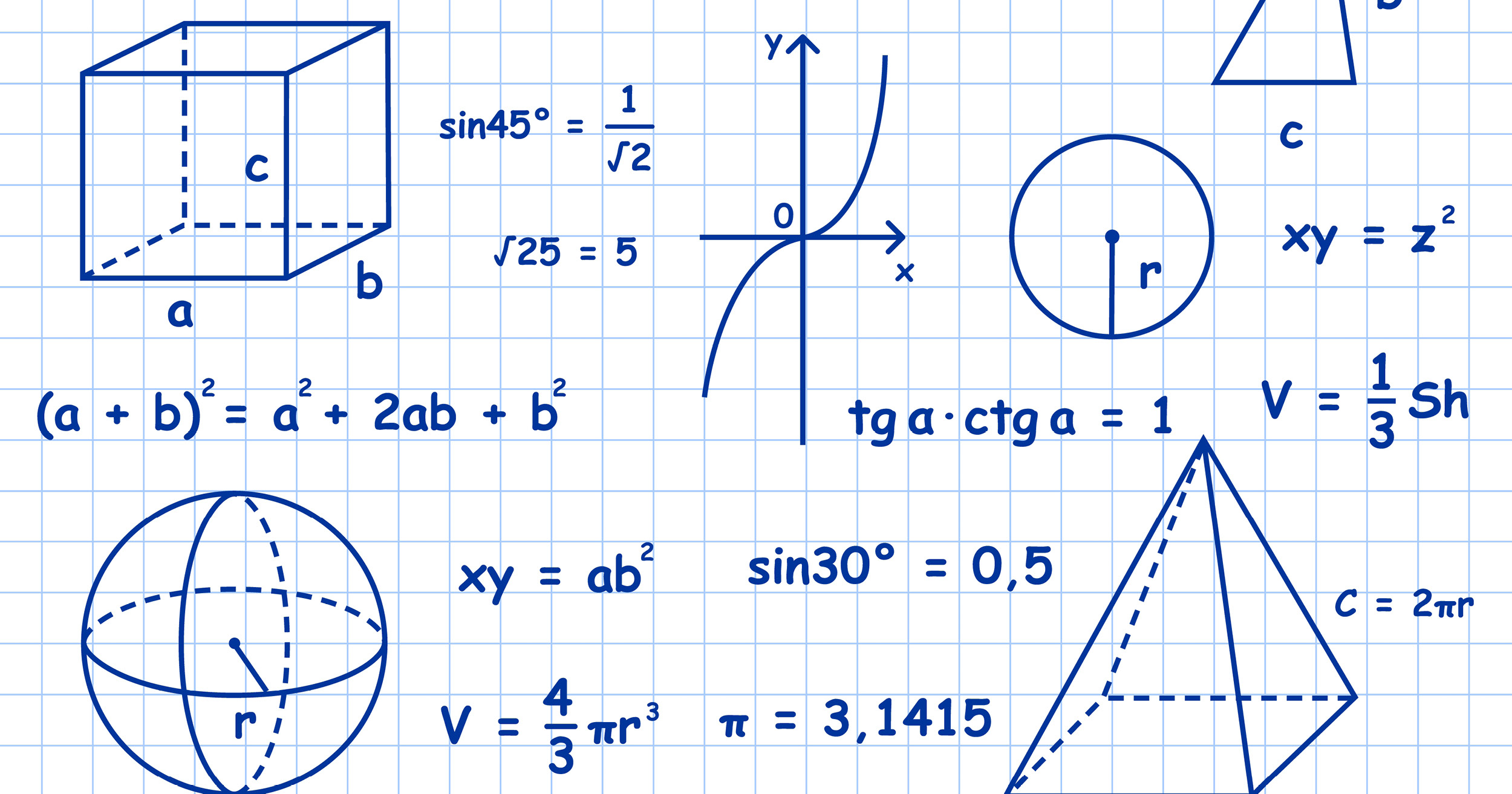
Geometrie ist eine der ältesten mathematischen Zweige und spielt eine entscheidende Rolle bei der Beschreibung und Berechnung von Formen, Figuren und Strukturen. Eine wichtige Komponente der Geometrie sind die geometrischen Formeln, welche uns helfen, Längen, Flächen, Volumen und andere Eigenschaften von Objekten zu bestimmen. Im Folgenden werden wir uns mit einigen grundlegenden geometrischen Formeln befassen und ihre Anwendungen in verschiedenen Bereichen erkunden.

Fläche und Umfang:

Rechteck:

Fläche: A = Länge x Breite
Umfang: U = 2 x (Länge + Breite)

Quadrat:

Fläche: A = Seite x Seite
Umfang: U = 4 x Seite

Dreieck:

Fläche: A = (Grundseite x Höhe) / 2
Umfang: U = Seite1 + Seite2 + Seite3

Kreis:

Fläche: A = π x Radius² (π ≈ 3,14159)
Umfang: U = 2 x π x Radius

Volumen:

Quader:

Volumen: V = Länge x Breite x Höhe

Zylinder:

Volumen: V = π x Radius² x Höhe

Kugel:

Volumen: V = (4/3) x π x Radius³

Satz des Pythagoras:

Der berühmte Satz des Pythagoras ist eine grundlegende geometrische Beziehung, die in vielen Anwendungen benötigt wird. Er besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Hypotenuse (die Seite gegenüber dem rechten Winkel) gleich der Summe der Quadrate der beiden anderen Seiten ist.

Satz des Pythagoras: a² + b² = c²

Anwendungen geometrischer Formeln:

Architektur und Bauwesen:

Bei der Planung von Gebäuden und Konstruktionen sind geometrische Formeln unerlässlich, um Maße, Flächen und Volumina richtig zu berechnen.

Ingenieurwesen:

Im Ingenieurwesen werden geometrische Formeln verwendet, um Strukturen wie Brücken, Straßen und Maschinen zu entwerfen und zu analysieren.

Naturwissenschaften:

In den Naturwissenschaften spielen geometrische Formeln eine wichtige Rolle bei der Berechnung von Volumen, Oberflächen und anderen Eigenschaften von Materialien und Objekten.

Grafikdesign und Kunst:

Künstler und Designer nutzen geometrische Formen, um harmonische Kompositionen zu schaffen und Proportionen in ihren Werken auszubalancieren.

Kartografie und Navigation:

Bei der Erstellung von Karten und bei der Navigation auf See oder in der Luft sind geometrische Formeln von entscheidender Bedeutung. Sie ermöglichen die genaue Messung von Entfernungen, Winkeln und Richtungen.

Computergrafik und Animation:

In der Welt der digitalen Visualisierung werden geometrische Formeln verwendet, um 3D-Modelle zu erstellen, Texturen zu kartieren und realistische Animationen zu generieren.

Datenanalyse und Statistik:

Geometrische Formeln finden auch Anwendung in der Datenanalyse und Statistik, um Muster, Trends und Beziehungen zwischen verschiedenen Variablen zu untersuchen.

Geometrische Formeln sind das Fundament der geometrischen Berechnungen und ermöglichen es uns, die Eigenschaften und Dimensionen von Objekten präzise zu bestimmen. Ein Verständnis der grundlegenden geometrischen Formeln ist essentiell, um die Welt um uns herum zu messen, zu gestalten und zu analysieren. Indem wir die Macht der geometrischen Formeln nutzen, können wir eine breite Palette von Problemen lösen und unsere Umgebung besser verstehen.

10 Beispiel Matheaufgaben mit geometrischen Formeln:

1. Aufgabe:
   Berechne die Fläche und den Umfang eines Rechtecks mit den Maßen Länge = 8 cm und Breite = 5 cm.
2. Aufgabe:
   Ein Quadrat hat eine Seitenlänge von 10 cm. Bestimme seine Fläche und seinen Umfang.
3. Aufgabe:
   Ein gleichseitiges Dreieck hat eine Seitenlänge von 12 cm. Berechne seine Fläche und seinen Umfang.
4. Aufgabe:
   Ein Kreis hat einen Radius von 6 cm. Ermittle seine Fläche und seinen Umfang. (Verwende π ≈ 3.14159)
5. Aufgabe:
   Ein Quader hat die Maße Länge = 10 cm, Breite = 6 cm und Höhe = 4 cm. Bestimme sein Volumen
6. Aufgabe:
   Ein Zylinder hat einen Radius von 5 cm und eine Höhe von 8 cm. Berechne sein Volumen. (Verwende π ≈ 3.14159)
7. Aufgabe:
   Eine Kugel hat einen Radius von 3 cm. Ermittle ihr Volumen. (Verwende π ≈ 3.14159)
8. Aufgabe:
   In einem rechtwinkligen Dreieck sind die beiden Katheten 7 cm und 9 cm lang. Berechne die Länge der Hypotenuse unter Verwendung des Satzes des Pythagoras.
9. Aufgabe:
   Ein Trapez hat eine parallele Seite von 12 cm, eine andere parallele Seite von 8 cm und eine Höhe von 5 cm. Bestimme seine Fläche.
10. Aufgabe:
    Ein regelmäßiges Fünfeck hat eine Seitenlänge von 6 cm. Berechne seine Fläche.
    
    

Lösungen:

1. Lösung:
   Fläche = Länge x Breite = 8 cm x 5 cm = 40 cm² Umfang = 2 x (Länge + Breite) = 2 x (8 cm + 5 cm) = 26 cm
2. Lösung:
   Fläche = Seitenlänge x Seitenlänge = 10 cm x 10 cm = 100 cm² Umfang = 4 x Seitenlänge = 4 x 10 cm = 40 cm
3. Lösung:
   Fläche = (√3 / 4) x Seitenlänge² = (√3 / 4) x 12 cm x 12 cm ≈ 62.35 cm² Umfang = 3 x Seitenlänge = 3 x 12 cm = 36 cm
4. Lösung:
   Fläche = π x Radius² = 3.14159 x 6 cm x 6 cm ≈ 113.1 cm² Umfang = 2 x π x Radius = 2 x 3.14159 x 6 cm ≈ 37.7 cm
5. Lösung:
   Volumen = Länge x Breite x Höhe = 10 cm x 6 cm x 4 cm = 240 cm³
6. Lösung:
   Volumen = π x Radius² x Höhe = 3.14159 x 5 cm x 5 cm x 8 cm ≈ 628.32 cm³
7. Lösung:
   Volumen = (4/3) x π x Radius³ = (4/3) x 3.14159 x 3 cm x 3 cm x 3 cm ≈ 113.1 cm³
8. Lösung:
   Hypotenuse² = Kathete₁² + Kathete₂² Hypotenuse² = 7 cm x 7 cm + 9 cm x 9 cm Hypotenuse² = 49 cm² + 81 cm² Hypotenuse² = 130 cm² Hypotenuse ≈ √130 cm ≈ 11.4 cm
9. Lösung:
   Fläche = (Summe der parallelen Seiten / 2) x Höhe Fläche = (12 cm + 8 cm) / 2 x 5 cm Fläche = 10 cm x 5 cm = 50 cm²
10. Lösung:
    Fläche = (5/4) x Seitenlänge² x cot(π/5) Fläche = (5/4) x 6 cm x 6 cm x cot(π/5) Fläche ≈ 27.527 cm²

Unser Artikel über geometrischen Formeln reicht nicht aus und dein Kind benötigt zusätzliche schulische Unterstützung? Dann schau bei avidii vorbei und überzeuge dich von unserer Online-Nachhilfe auf Spitzenniveau. Jetzt kostenlos testen!